Теперь, когда есть представление о том, что такое децибелы, логарифмы, действия с логарифмами и логарифмические таблицы, можно приступить к рассмотрению правил сложения уровней интенсивности звуков.
Выше было дано определение уровню интенсивности (силы) звука и сказано, что эта величина измеряется в децибелах.
Было также дано разъяснение, что децибел не является физической величиной.
Децибел − это десятичный логарифм, т.е. величина чисто математическая, подчиняющаяся математическим (см. Раздел 2), а не физическим законам.
Поэтому при совместном действии двух и более источников звука (шума) результи­рующий уровень интенсивности (силы) звука не может быть выражен простым сложением их физических характеристик. Необходимо находить логарифмы суммы их интенсивности или квадратов их звуковых давлений, пользуясь формулой (30):

По данным Герхарда Молля, приведем несколько своеобразных при­меров такого сложения:

1дБ + 1дБ = 3дБ
70дБ + 70дБ = 73дБ
50дБ + 50дБ + 50дБ + 50дБ = 56дБ
Историческая справка
Gerhard Moll, (1785—1838) — проф. физики и HматематикиH, HдиректорH обсерватории в Утрехте. Работы его относятся преимущественно к электромагнетизму. Чаще цитируется его HисследованиеH, произведенное им в 1823 г. вместе с Van Beck над скоростью звука. Полученный ими результат для скорости звука в сухом воздухе при 0° — 332,25 м/c — считается одним из наиболее точных.

Эти примеры, хотя и очень наглядные, по форме записи не вполне правильные. Правильно записать их в виде формулы (31), имеющей большое практическое значение:

где,
Li − уровни звукового давления источников шума
n − количество источников шума

Рассмотрим эту формулу более подробно применительно к результирующему уровню интенсивности звука двух источников звука, одновременно работающих c одинаковой интенсивностью  (бел).
Для решения этой задачи введём некоторые обозначения:

L1 − уровень интенсивности звука первого источника звука (дБ).
L2 − уровень интенсивности звука второго источника звука (дБ).
Lрез − искомый результирующий уровень звука (дБ).
L1 = L2 = 10 (дБ) − основное условие задачи (дБ).
Руководствуясь формулой (31) мы вправе записать и решить логарифмическое уравнение:

Увеличение в два раза количества источников звука, имеющих одинаковый уровень звука,
 приводит к повышению общего уровня интенсивности (силы) звука только на 3 дБ.
Это утверждение справедливо для любого уровня интенсивности звука.

Из этого утверждения и формулы (31) следует, что при n одинаковых источниках шума с уровнями Li результирующий уровень шума в децибелах (дБ) равен (формула 32):

Lрез = Li + 10•lgn             (32)
UПримеры

• При

n = 4 и Li = 50дБ
Lрез = Li + 10•lgn= 50 + 10•lg4 ≈ 50 + 10•6 = 56дБ

• При одновременной работе четырех мотоцик­летных двигателей, уровень звукового давления каждого из которых составляет 80дБ, результирующий уровень составит 86дБ. После отъезда двух мотоциклов результирующий уровень звукового давления снизится всего на 3дБ и составит 83дБ.

Весьма интересным и, на первый взгляд, противоречивым является тот факт, что два одинаково громких источника звука при их совместном действии на слух ощущаются не так громко, как удвоен­ный по громкости одиночный источник звука.
Попробуем это объяснить, исходя из приведённых выше формул.
Мы определили, что при удвоении количества источников звука, работающих с одинаковой интенсивностью, результирующий уровень интенсивности увеличится только на 3 децибела (дБ).
Допустим у нас есть источник звука, работающий с уровнем интенсивности  равным L1 (дБ).
Вопрос:
Как измениться уровень интенсивности звука этого источника (дБ), если увеличить интенсивность его звучания, например, в два раза.
Сокращённо условия задачи можно записать следующим образом:

I1 − первоначальная интенсивность источника звука.
P1− первоначальное звуковое давление.
I2 − изменённая интенсивность источника звука.
P2 − звуковое давление после изменения.
L1 − первоначальный уровень интенсивности звука источника звука (дБ).
L2 − изменённый уровень интенсивности звука источника звука (дБ).
I2  = 2I1− основное условие задачи

Поскольку мы имеем один источник звука воспользуемся пропорциональностью  (21) и формулой (30), запишем:

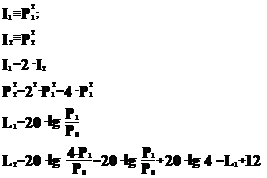
UОтвет:U Уровень интенсивности звука при удвоении его интенсивности увеличивается на 12 дБ

 При удвоении интенсивности звука одного источника результирующий уровень интенсивности его звука увеличивается на 12 дБ.

Сравним этот результат с результатом, который мы получили до этого.
Действительно, наглядно видно, что:

• удвоение громкости звучания одного источника звука приводит к приросту результирующего уровня звука на 12 дБ
• увеличение в два раза количества одинаково звучащих источников звука приводит к приросту результирующего уровня звука только на 3 дБ.

UРис. 8U

Изменение уровня интенсивности звука в зависимости от звукового давления

В этой связи можно сделать вывод:

Несмотря на свою не физическую, а чисто математическую сущность, увеличение  уровня интенсивности звука (дБ), абсолютно точно характеризует экспоненциальный прямолинейный  рост интенсивности звука, в зависимости от  роста звукового давления, реально воспринимаемого слухом человека (см.  Рис 8)

Сложение уровней интенсивности звука (с точностью ±0,5дБ)
UТаблица №6U
Разность между двумя уровнями (дБ)	Прибавка к более высокому уровню (дБ)
0	3
1	2,5
2	2
3	2
4	1,5
5	1
6	1
7	1
8	0,5
9	0,5
10	0

Исходя из изложенного, при наличии источников шумов разной интенсивности необходимо избавиться прежде всего от источника наиболее громких шу­мов.
Большое практическое значение имеет понимание того, как воспринимает слух человека изменение уровня интенсивности, выраженный в децибелах, при сложении звуков различной интенсивности.
Для понимания нашей темы важно иметь представление о том, в какой зависимости находятся интенсивность, звуковое давление и уровень звука.
В порядке иллюстрации воспользуемся таблицами и примерами из книги английского инженера                 Р. Тейлора «Шум» (см. Таблицы №6 и №7).

Интенсивность, звуковое давление и уровень звука в воздухе при комнатной температуре и нормальном давлении на уровне моря
UТаблица №7U
Интенсивность, вт/м2			Звуковое давление, Н/м2			Уровень звука, дб
100 000 000			200 000			200
10 000 000						190
1 000 000			20 000			180
100 000						170
10 000			2 000			160
1 000						150
100			200			140
10						130
1			20			120
	0,1					110
	0,01		2			100
	0,001					90
	0,000 1			0,2		80
	0,000 01					70
	0,000 001			0,02		60
	0,000 000 1					50
	0,000 000 01			0,002		40
	0,000 000 001					30
	0,000 000 000 1			0,000 2		20
	0,000 000 000 01					10
	0,000 000 000 001			0,000 02		0

Анализируя таблицу №6, легко придти к следующему выводу

В случае двух источников звука максимальная прибавка к более высокому уровню интенсивности звука возникает при условии отсутствия разности между уровнями звука этих источников.

Анализ таблицы №7 позволяет сделать другое немаловажное заключение.

Диапазон звуковых давлений не так широк, как диапазон интенсивностей: звуковое давление возрастает вдвое медленнее, чем интенсивность.

Выражая  уровень звукового давления в децибе­лах, следует помнить:

при увеличении давления вдвое интенсивность увеличивается на 6 дБ.

Поясним это следующим примером.
UПример.
В кабине грузового автомобиля измерено звуковое давление, которое составило 2 Н/м2.
Мы знаем, что звуковое давление самого слабого из слышимых звуков составляет 2•10-5.
Воспользовавшись формулой (30), определяем уровень интенсивности шума в кабине.
Он составит:

Мы знаем, что при увеличении звукового давления вдвое прибавляется 6дБ.
Поэтому, если в кабине грузовика уровень интенсивности шума увеличится до 106дБ, звуковое давление составит 4 Н/м2, а интенсивность звука увеличится в четыре раза и достигнет 0,04 вт/м2.

Итак, мы ознакомились с основными объективными и субъективными понятиями, принятыми в акустике.

Назад к разделам